How Many Sides Does a Polygon Have? Unravel the Mystery
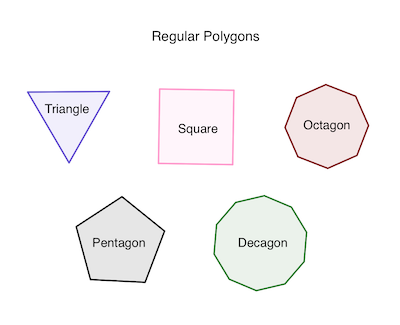
How Many Sides Does a Polygon Have? A polygon has multiple sides, the exact number depending on the specific shape. Generally, a polygon can have three or more sides, making it a closed figure formed by straight lines.
Each side connects two consecutive vertices, or corners, of the polygon. The simplest polygon is a triangle, which has three sides. As the number of sides increases, polygons can be classified as quadrilaterals (four sides), pentagons (five sides), hexagons (six sides), and so on.
The term “polygon” is derived from the Greek words “poly,” meaning many, and “gonia,” meaning angle. Polygons are widely studied in geometry and have various applications in fields such as architecture, engineering, and computer graphics.
The Basics Of Polygons
Polygons are geometric shapes with straight sides. The number of sides in a polygon can vary, ranging from three sides in a triangle to infinite sides in a circle. Each polygon has a unique set of angles and properties based on its number of sides.
Defining Polygons
How many sides does a Polygon have? Polygons are two-dimensional shapes that consist of straight lines. These lines connect to form a closed shape, and each line segment is called a side. The sides meet at points called vertices. Polygons can have any number of sides, but they must have at least three sides to be considered a polygon.
Characteristics Shared By All Polygons
All polygons have certain characteristics in common. These include:
- Sides: As mentioned, polygons have straight sides, and these sides meet at vertices.
- Angles: The angles formed by the sides of a polygon add up to 360 degrees.
- Interior: The interior of a polygon is the space inside the shape, and the exterior is the area outside of the shape.
- Area: The area of a polygon is the measure of the space inside the shape.
- Perimeter: The perimeter of a polygon is the sum of the lengths of its sides.
In conclusion, polygons are fascinating shapes that have a variety of uses in math and the world around us. Understanding the basics of polygons is crucial for anyone working with geometry or interested in learning more about this topic.

Credit: www.flickr.com
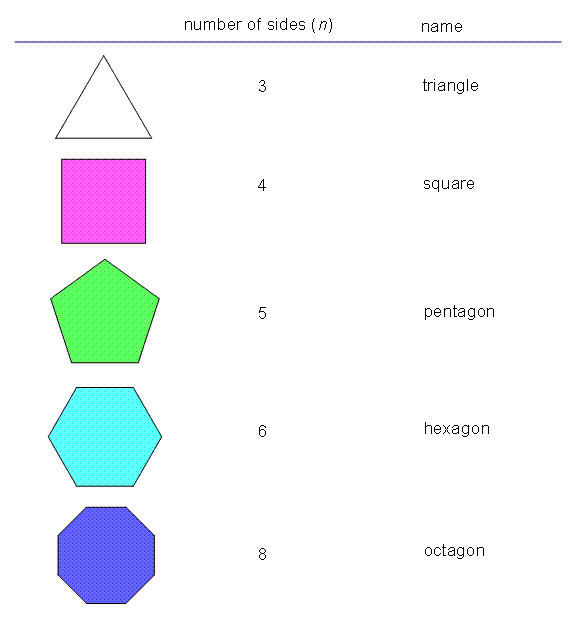
Polygon Classification By Sides
A polygon is classified by the number of sides it has, which can vary from three to infinity. The number of sides determines the type of polygon, such as a triangle (3 sides), quadrilateral (4 sides), or pentagon (5 sides).
Different polygons exhibit unique properties based on their side counts.
Triangles, Quadrilaterals, Pentagons, and Hexagons are common polygons. Each type has unique characteristics based on the number of sides.
Triangles: The Simplest Polygons
Triangles have three sides and three angles. They are the simplest type of polygons.
Quadrilaterals: Four-sided Figures
Quadrilaterals have four sides and four angles. Examples include squares, rectangles, and parallelograms.
Pentagons And Hexagons: Beyond The Basics
Pentagons have five sides, while hexagons have six sides. They are more complex polygons.
The Infinite Possibilities
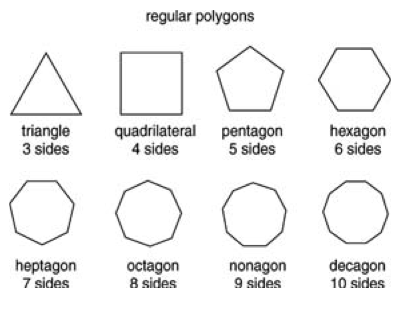
When we think about polygons, we often imagine shapes with a specific number of sides. However, the world of polygons is far more diverse and fascinating than we might think. From heptagons to decagons and beyond, polygons have an infinite number of possibilities.
From Heptagons To Decagons
Heptagons, also known as seven-sided polygons, are intriguing shapes that can add an artistic touch to any design. With their angular edges and symmetrical structure, heptagons are visually pleasing and can be found in various natural and man-made objects. Imagine a captivating stained glass window or a unique garden trellis, both adorned with heptagonal patterns.
Octagons, with their eight sides, are commonly found in architecture, especially in the design of buildings and bridges. Their sturdy structure and evenly distributed sides make octagons an ideal choice for creating stable and visually appealing structures.
Nonagons, or nine-sided polygons, offer a perfect balance between complexity and simplicity. With their unique shape, nonagons can be used to create stunning mosaics or decorative tiles, adding an artistic flair to any space.
Decagons, as the name suggests, are polygons with ten sides. These shapes are often used in geometric patterns and tessellations, where they can create intricate and mesmerizing designs. From ancient Islamic art to modern-day architectural marvels, decagons have stood the test of time as a symbol of beauty and harmony.
The World Of N-gons
As we explore the world of polygons, we encounter a fascinating concept: n-gons. An n-gon is a polygon with an indefinite number of sides, allowing for endless possibilities. Whether it’s a triangle (a 3-gon), a hexagon (a 6-gon), or a dodecagon (a 12-gon), the term “n-gon” encompasses all polygons, regardless of the specific number of sides they possess.
With n-gons, the possibilities truly become infinite. From simple shapes to complex configurations, n-gons can be used in various fields, such as mathematics, art, and design. Their versatility allows for endless creativity, making them a favorite among artists, architects, and mathematicians alike.
In conclusion, the world of polygons offers a rich tapestry of shapes and possibilities. From heptagons to decagons and the ever-expanding realm of n-gons, polygons continue to captivate our imagination and inspire us to explore the beauty of geometry.
Regular Vs. Irregular Polygons
Regular polygons have equal sides and angles, while irregular polygons have different side lengths and angles. The number of sides in a polygon can vary, ranging from three to infinity. Each polygon has its unique characteristics and properties, making them fascinating shapes to explore.
Regular vs. Irregular Polygons: When it comes to polygons, it’s essential to understand the difference between regular and irregular polygons. Regular polygons have equal sides and equal angles, while irregular polygons have sides and angles of varying lengths and measurements.
In this section, we will dive deeper into the characteristics of each type of polygon. Identifying Regular Polygons: Regular polygons are easy to identify because they have a uniform shape and size. For example, a square is a regular polygon because all four sides and angles are equal. Similarly, an equilateral triangle is also a regular polygon because all three sides and angles are equal.
In general, any polygon with equal sides and angles is a regular polygon. The Diversity of Irregular Polygons: Irregular polygons, on the other hand, come in a wide variety of shapes and sizes. They can have sides and angles of any length or measurement, making them more challenging to identify than regular polygons. Some examples of irregular polygons include a pentagon, hexagon, or octagon with sides of varying lengths and angles that are not equal. To better understand the difference between regular and irregular polygons, let’s compare them side by side:
| Regular Polygons | Irregular Polygons |
|---|---|
| Equal sides and angles | Varying sides and angles |
| Uniform shape and size | Wide variety of shapes and sizes |
| Easy to identify | Challenging to identify |
In conclusion, understanding the difference between regular and irregular polygons is crucial for anyone studying geometry. By identifying the characteristics of each type of polygon, you can better understand their properties and use them in various mathematical equations.
Mathematical Formulas For Polygon Sides
Calculating Interior Angles
A polygon’s interior angles can be calculated using the formula: Interior Angle = (n-2) 180 / n, where n represents the number of sides in the polygon.
The Sum Of Exterior Angles
The sum of a polygon’s exterior angles is always 360 degrees. Each exterior angle of a polygon can be calculated using the formula: Exterior Angle = 360 / n, where n is the number of sides in the polygon.
Credit: socratic.org
Polygons In Nature And Technology
In both nature and technology, polygons play a significant role in shaping our world. From the intricate patterns found in natural occurrences to the precise designs used in architectural masterpieces, polygons are everywhere. Let’s explore the various ways polygons manifest themselves in nature and technology.
Natural Occurrences Of Polygons
When it comes to the natural world, polygons can be observed in various forms, showcasing the beauty of mathematical principles in action. Here are some examples:
- Crystals: Many crystals, such as quartz and salt, form in geometric shapes with polygonal faces. These structures are a result of the repeating arrangement of atoms or molecules.
- Honeycombs: Bees construct their hives in the form of hexagonal honeycomb cells. This shape allows for efficient use of space, maximizing storage capacity.
- Snowflakes: Each unique snowflake is a delicate hexagonal crystal. The intricate patterns they form are a testament to the symmetry and beauty found in nature.
Polygons In Architectural Design
In architectural design, polygons are utilized to create visually appealing and structurally sound buildings. Here are some ways polygons are incorporated:
- Facade Designs: Many modern buildings feature facades with polygonal patterns. These designs not only enhance the aesthetic appeal but also provide strength and stability to the structure.
- Domes and Arches: Domes and arches in architectural marvels like the Pantheon and Taj Mahal rely on polygonal shapes for their structural integrity. The use of polygons distributes weight evenly, ensuring the stability of these iconic structures.
- Skylights and Windows: Polygonal shapes are often used in skylights and windows to allow optimal light penetration while maintaining a visually pleasing appearance.
Polygons In Technology
Technology heavily relies on polygons for various applications. Here are some examples:
- Computer Graphics: Polygons are fundamental components in computer graphics, where they are used to create 3D models and render realistic images.
- Geographic Information Systems (GIS): In GIS, polygons are used to represent and analyze geographic features such as land parcels, boundaries, and regions.
- Printed Circuit Boards (PCBs): PCBs, commonly used in electronic devices, often have polygonal copper traces connecting various components, ensuring efficient electrical conductivity.
Polygons are not only a mathematical concept but a fundamental part of our world. From the elegance of natural occurrences to the precision of architectural design and technology, polygons continue to shape and influence our lives.
Creating Polygons: A Step-by-step Guide
Discover the step-by-step process of creating polygons and unravel the mystery of how many sides a polygon can have. From triangles to decagons, this guide provides a clear and concise explanation of the diverse range of polygon shapes, making it easy to understand and apply in various mathematical and design contexts.
Drawing Perfect Polygons
Creating polygons involves connecting points to form closed shapes. Polygons can have various sides, such as triangles, squares, or octagons. Begin by plotting the vertices of the polygon on a piece of paper. Use a ruler to draw straight lines between the vertices. Ensure each line meets at the endpoints to form a closed shape.
Using Technology To Construct Polygons
Various online tools can help in constructing accurate polygons. Software like Adobe Illustrator allows for precise polygon creation. Input the coordinates of the vertices to generate a polygon. Technology simplifies the process by automating the shape creation. Check for any errors and make adjustments as needed.
The Significance Of Polygons In Modern Mathematics
Polygons In Geometric Theorems
Polygons play a vital role in geometric theorems.
- Help prove essential concepts in geometry.
- Form the foundation of geometric principles.
- Assist in understanding spatial relationships.
Applications Of Polygons In Advanced Mathematics
Polygons have diverse applications in advanced mathematics.
- Used in calculus, algebra, and trigonometry.
- Applied in computer graphics and data analysis.
- Utilized in optimization problems and physics equations.
Credit: americanboard.org
Frequently Asked Questions
How Many Sides Does A Polygon Have?
A polygon can have a minimum of three sides and a maximum of infinite sides. The number of sides in a polygon is determined by the number of straight sides it has. Each side connects two vertices, and the total number of sides contributes to the polygon’s shape and classification.
What Is The Name Of A 10-sided Polygon?
A 10-sided polygon is called a decagon. It is a two-dimensional shape with ten straight sides and ten angles. Decagons are often used in architecture, design, and geometry due to their symmetrical and distinctive characteristics.
Can A Polygon Have An Odd Number Of Sides?
Yes, a polygon can have an odd number of sides. For example, a pentagon has five sides, a heptagon has seven sides, and a nonagon has nine sides. The classification of polygons is based on the number of sides and angles, and odd numbers are common in polygon formations.
Conclusion
Understanding the number of sides a polygon has is essential for various applications. By learning the characteristics of different polygons, we can enhance our problem-solving skills and spatial awareness. Whether it’s for mathematical calculations or real-world scenarios, knowing the sides of polygons is valuable in many aspects of our lives.





