How Many Triangles: Unraveling the Mystery

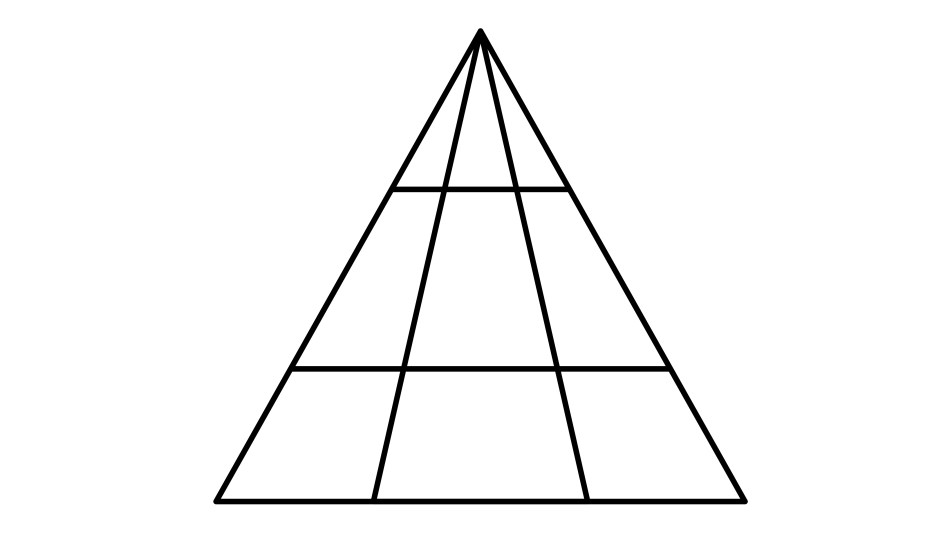
How Many Triangles? There are a total of 16 triangles within the given figure. In this blog post, we will explore the concept of counting triangles and discuss various methods to accurately determine the number of triangles in a given figure.
Understanding how to count triangles can be useful in geometry, puzzle-solving, and pattern recognition. By following a systematic approach, we can break down the figure into smaller components and identify all the triangles. Whether you are a student studying geometry or someone who enjoys solving puzzles, mastering the skill of counting triangles will enhance your problem-solving abilities.
So, let’s dive in and discover the fascinating world of triangles!
Credit: www.womansworld.com
The Intrigue Of Triangle Puzzles
Triangle puzzles have been around for centuries, and they continue to fascinate people of all ages. There is something about the challenge of figuring out how many triangles are hidden within a larger triangle that appeals to our cognitive abilities. In this blog post, we will explore the cognitive appeal of triangle puzzles, as well as their popularity in brain teasers.
Cognitive Appeal
The human brain is wired to recognize patterns and shapes, which makes solving triangle puzzles particularly appealing. When we look at a larger triangle, we automatically start breaking it down into smaller shapes, trying to identify any triangles that might be hiding within. This process engages our visual-spatial reasoning skills and challenges our problem-solving abilities.
Popularity In Brain Teasers
Triangle puzzles are a staple in brain teasers and IQ tests. They are often used to test a person’s ability to think critically and solve complex problems. The popularity of triangle puzzles in these types of tests is a testament to their effectiveness in challenging our cognitive abilities.
Overall, triangle puzzles are a fun and challenging way to exercise our minds. Whether you’re solving them for fun or as part of a brain teaser, they offer a unique and engaging mental workout that can help keep our minds sharp.

Credit: www.youtube.com
Historical Perspective
The historical perspective of the How Many Triangles problem offers a fascinating glimpse into its evolution over time.
Ancient Origins
Ancient civilizations, like the Babylonians and Egyptians, explored geometric concepts related to triangles.
Early mathematicians laid the groundwork for triangle calculations that influence modern math.
Modern Adaptations
Today, the How Many Triangles challenge has found new life in recreational math circles.
It has also been integrated into educational settings to enhance spatial reasoning skills.
Basic Concepts In Triangle Counting
Understanding the basic concepts in triangle counting is essential for solving complex geometric problems. Whether you are a math enthusiast or simply curious about the fascinating world of triangles, this article will guide you through the fundamental aspects of triangle classification and properties.
Types Of Triangles
Triangles can be classified into different types based on their side lengths and angles:
| Type | Description |
|---|---|
| Equilateral Triangle | A triangle with all sides of equal length |
| Isosceles Triangle | A triangle with two sides of equal length |
| Scalene Triangle | A triangle with no sides of equal length |
| Right Triangle | A triangle with one right angle (90 degrees) |
| Obtuse Triangle | A triangle with one obtuse angle (greater than 90 degrees) |
| Acute Triangle | A triangle with three acute angles (less than 90 degrees) |
Properties Of Triangles
Triangles possess various properties that contribute to their unique characteristics:
- Sum of Angles: The sum of the three interior angles of a triangle is always 180 degrees.
- Pythagorean Theorem: In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides.
- Area: The area of a triangle can be calculated using the formula: (base height) / 2.
- Perimeter: The perimeter of a triangle is the sum of the lengths of its three sides.
- Congruence: Two triangles are congruent if their corresponding sides and angles are equal.
Understanding these basic concepts will lay a solid foundation for further exploration into the fascinating world of triangle counting. Whether you are solving geometry problems or simply appreciating the elegance of triangles, these fundamental concepts will prove invaluable.
Strategies For Solving Triangle Puzzles
Discover effective strategies for solving triangle puzzles and determining the number of triangles involved. These techniques will help you approach the problem with clarity and precision, enabling you to find the correct answer efficiently.
Triangle puzzles are a great way to challenge your brain and improve your problem-solving skills. However, it can be frustrating when you can’t seem to find all the triangles in a puzzle. That’s why it’s important to have some strategies to help you solve these puzzles more efficiently. Here are some systematic approaches to help you find all the triangles in a puzzle.
Pattern Recognition
One of the best ways to find all the triangles in a puzzle is to look for patterns. Patterns are a great way to quickly identify triangles in a puzzle. Look for triangles that are similar in size and shape, or that have a common vertex. You can also look for triangles that are formed by lines that intersect at a right angle.
Systematic Approaches
Another strategy for solving triangle puzzles is to use a systematic approach. Start by looking for the largest triangles in the puzzle, then work your way down to the smaller ones. You can also look for triangles that are formed by lines that are parallel or perpendicular to each other. Try to break the puzzle down into smaller sections and solve each section one at a time.
Table: Triangle Puzzle Strategies
| Strategy | Description |
|---|---|
| Pattern Recognition | Look for patterns to quickly identify triangles in the puzzle. |
| Systematic Approaches | Use a systematic approach to break the puzzle down into smaller sections and solve each section one at a time. |
Ordered List: Tips for Solving Triangle Puzzles
- Start by looking for the largest triangles in the puzzle.
- Use patterns to quickly identify triangles.
- Break the puzzle down into smaller sections and solve each section one at a time.
- Look for triangles that are formed by lines that are parallel or perpendicular to each other.
Unordered List: Strategies for Triangle Puzzle Solving
- Look for patterns
- Start with the largest triangles
- Use a systematic approach
- Break the puzzle down into smaller sections
- Look for triangles formed by parallel or perpendicular lines
In conclusion, triangle puzzles can be challenging, but with these strategies, you’ll be able to solve them more efficiently. Whether you’re using pattern recognition or a systematic approach, the key is to break the puzzle down into smaller sections and solve each section one at a time. With a little practice, you’ll be able to find all the triangles in a puzzle in no time!
Challenges And Variations
Increasing Complexity
As you delve into the world of counting triangles, you’ll encounter increasingly complex puzzles that will test your spatial reasoning and pattern recognition abilities. These challenges involve intricate arrangements of lines and shapes, requiring you to think critically and systematically in order to identify all the triangles within the given structure.
Famous Triangle Puzzles
Some of the most famous triangle puzzles have captivated enthusiasts for generations. From the classic “Triangle within a Triangle” to the intriguing “Triangle Grid Patterns,” these puzzles offer a fascinating and enjoyable way to hone your problem-solving skills and have fun at the same time.
Mathematical Formulas And Theorems
Mathematical formulas and theorems provide a systematic approach to solving problems involving shapes. When it comes to determining how many triangles can be formed within a given shape, there are specific formulas and theorems to apply. By using these mathematical principles, you can efficiently calculate the number of triangles without extensive manual counting.
Geometric Principles
Geometric principles play a crucial role in determining the number of triangles in a given figure. By understanding these principles, we can apply the relevant formulas and theorems to calculate the number of triangles accurately. Let’s take a closer look at some of the key geometric principles involved. One of the fundamental concepts is that a triangle is formed by connecting three non-collinear points.
This means that any three points that do not lie on the same line can be used to create a unique triangle. By identifying these points within a figure, we can start counting the number of triangles. Another important principle is the concept of triangles within triangles. This occurs when a larger triangle contains smaller triangles within its boundaries. By identifying these nested triangles, we can count them individually and include them in our total count.
Combinatorics And Counting
Combinatorics and counting techniques also play a significant role in determining the number of triangles. These mathematical methods help us calculate the total number of possible combinations and permutations within a given figure. One such technique is the combination formula, often denoted as nCr, which calculates the number of ways to choose r objects from a set of n objects without considering their order.
In the context of triangles, this formula can be used to determine the number of ways to select three points from a given set of points. Another counting technique is the principle of inclusion-exclusion. This principle allows us to calculate the total number of triangles by accounting for overlapping triangles. By subtracting the number of overlapping triangles from the total count, we can obtain an accurate number.
To summarize, understanding geometric principles and utilizing combinatorics and counting techniques are crucial when calculating the number of triangles in a figure. By applying these formulas and theorems, we can confidently determine the total count, taking into account nested triangles and potential overlaps.
Psychology Behind Puzzle Solving
Problem-solving Skills
Puzzle-solving enhances analytical thinking and creativity.
It boosts critical thinking and logical reasoning abilities.
The Satisfaction Of Discovery
Discovering solutions triggers a sense of accomplishment.
It provides a dopamine rush, leading to motivation.
Applications And Educational Benefits
Identifying the number of triangles in a given figure can be a fun and educational activity for students of all ages. This can help develop their spatial reasoning and critical thinking skills, while also improving their ability to visualize complex shapes.
By using interactive applications, students can learn and practice this skill in a fun and engaging way.
Teaching Geometry
Geometry concepts can be visually explained through triangle puzzles.
Students can learn about angles, sides, and shapes through triangles.
It helps in understanding the properties of triangles easily.
Enhancing Cognitive Abilities
Solving triangle puzzles sharpens critical thinking skills.
Identifying patterns in triangles boosts problem-solving abilities.
It enhances spatial awareness and geometric reasoning.
Interactive Triangle Puzzle Platforms
Exploring Interactive Triangle Puzzle Platforms offers a fun and engaging way to challenge your mind while enhancing your geometric skills. These platforms provide a variety of activities that cater to different age groups and skill levels.
Digital Games
Engage in exciting digital games that test your ability to identify and manipulate triangles. These games often feature vibrant graphics and intuitive controls, making learning enjoyable and interactive.
Educational Resources
Access a wealth of educational resources on triangle puzzles, including tutorials, worksheets, and quizzes. These resources are designed to help learners grasp triangle concepts effectively and reinforce their understanding through practice.
Concluding Thoughts
The number of triangles in a shape can be determined by using the formula n(n+1)/2, where n represents the number of sides. This simple equation provides an efficient way to calculate the total number of triangles, making it easier to analyze complex geometrical figures.
The Everlasting Appeal
The allure of solving the How Many Triangles puzzle lies in its simplicity and complexity.
It engages the mind and sharpens problem-solving skills in a fun way.
Encouraging Mathematical Curiosity
How Many Triangles sparks curiosity in numbers and geometric shapes.
It encourages exploration and experimentation with different solutions.
How Many Triangles is more than a puzzle; it’s a gateway to mathematical discovery.
It fosters a love for numbers and shapes in a playful and engaging manner.
Frequently Asked Questions
How Many Triangles Can Be Found In A Hexagon?
In a hexagon, you can find a total of 24 triangles. These include 18 smaller triangles formed by connecting the vertices, and 6 larger triangles created by connecting the midpoints of the sides.
What Is The Formula To Calculate The Number Of Triangles In A Polygon?
The formula to calculate the number of triangles in a polygon is n(n-1)(n-2)/6, where n represents the number of sides of the polygon. This formula applies to regular polygons, where all sides and angles are equal.
Can A Triangle Be Formed With Any Three Line Segments Within A Hexagon?
No, not every combination of three line segments within a hexagon can form a triangle. The segments must satisfy the triangle inequality theorem, where the sum of the lengths of any two sides must be greater than the length of the third side.
Conclusion
Understanding the concept of counting triangles can be challenging but rewarding. By using the methods discussed, you can confidently tackle triangle puzzles. Remember, practice makes perfect, so keep honing your skills. Now, go ahead and put your newfound knowledge to the test!





